
Çift ve Tek simetri sistemini incelerken Kur’ân’da bulunan aşağıdaki ayetler üzerinde düşünmeli ve aşağıdaki soruları kendimize sormalıyız.
Diyanet Meali:
89 – Fecr Suresi – Ayet 3: Çifte ve teke andolsun,
89 – Fecr Suresi – Ayet 5: Şüphesiz bunlarda, akıl sahibi bir kimse için üzerine yemin edilmeye değer bir özellik vardır.
75 – Kıyamet Suresi – Ayet 17: Şüphesiz onu toplamak ve okumak bize aittir.
- Çift ve Tek nedir? Allah Çift ve Tek’in üstüne neden yemin ediyor? “Yemin edilmeye değer bir özellik vardır” şeklinde ayrıca belirtiliyor. Nedir üzerine yemin edilecek, bu özellik?
- Allah “Şüphesiz onu toplamak bize aittir” şeklinde beyan etmiş. Bu “Toplamak” ifadesi ne anlama geliyor?
- Kur’ân neden Nuzül sırasında değil?!! Neden Nuzül sırasından değişik bir sıralamada Kur’ân fihristi karşımıza çıkıyor. Bu fihrist kimin tarafından oluşturulmuş (Toplanmış). Bu fihristin nasıl bir anlamı, önemi var. Veya önemi var mı? Önemi olmalı mı? Önemi varsa nedir?!!
Kur’ân bütününde bir sayısal sistem düşünülecek ise, ilk bakıldığında oluşturabileceğimiz bilgi grupları (Kümeler) aşağıdaki gibi karşımıza çıkar.
- Sureler (Sure numaraları)
- Ayetler (Numaralandırılmış ayet sayıları)
- Numarasız Besmeleler

Simetri sistemini basit olarak bu temel gruplar üzerinden araştırılabiliriz. Bu şekildeki ilk gözlemi Koroş Cemnişan (Kourosh Jamneshan) http://www.amazing19.com/ adlı İranlı bir üniversite öğrencisi yapmıştır. Bu çalışmada, sure numaraları ve ayet sayıları birer sayısal küme olarak düşünülmüş, numarasız besmeleler ise ayrı bir sayısal bir küme olarak görülmüş ve simetri sisteminde kullanılmamıştır. Sonuca bakılırsa sayısal gruplama (kümeler) doğru olarak belirlenmiştir.
Simetri hesapları Aşama-1: Ayet sayısı Çift ve Tek olan Surelerin sayıları (60 ve 54)
Ayet sayılarını bir sayı kümesi olarak düşünelim;
Ayet sayıları = { 7 , 286 , 200 , 176 , . . . , 4 , 5 , 6 } şeklinde 114 elemanlı bir küme oluşur. Yapılan iş, bu kümenin Çift ve Tek sayılarından oluşan alt kümelerin eleman sayılarının belirlenmesinden ibarettir.
Aşağıda alt kümeleri, başından ve sonundan bir bölümünü görebileceğiniz şekilde yazmaya çalıştım.
Ayet sayısı çift olanlar = { 286 , 200 , 176 , 120 , . . . , 4 , 6 }
Ayet sayısı tek olanlar = { 7 , 165 , 75 , 129 , 123 , . . . , 5 , 5 }
Bu kümelerin eleman sayıları;
Ayet sayısı çift olanların eleman sayısı = 60, yani 60 adet çift sayımız var.
Ayet sayısı tek olanların eleman sayısı = 54, yani 54 adet tek sayımız var.
60 + 54 = 114 olarak sonucu buluruz.
Aşağıdaki tabloda detayları bulabilirsiniz.
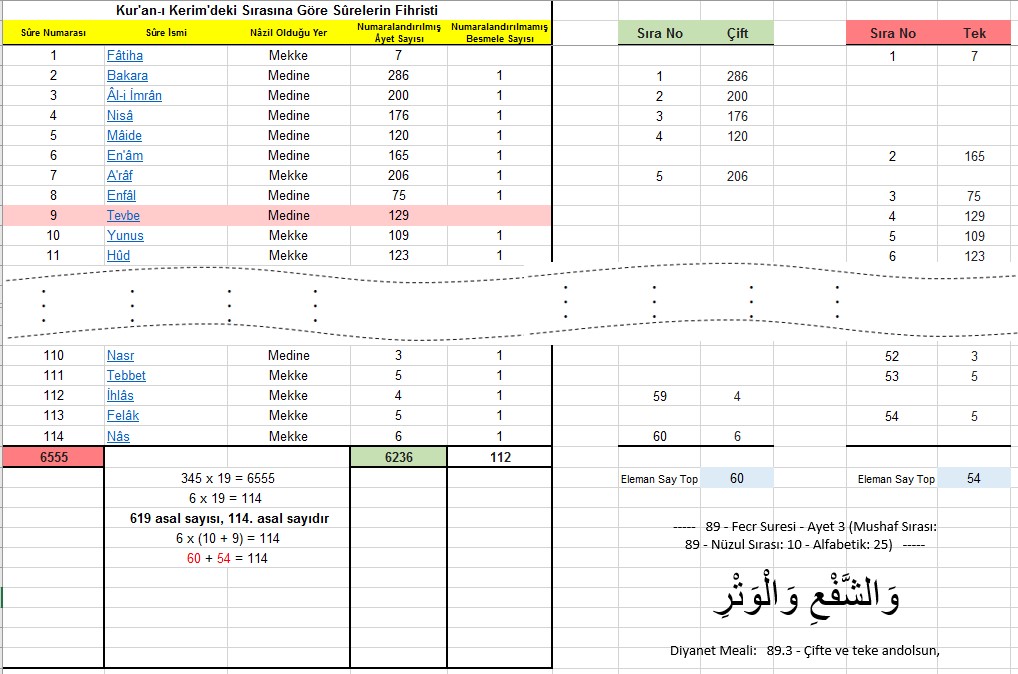
Burada karşımıza çıkan ilk ilginç durum, yukarıda elde ettiğimiz 60 ve 54 sayılarının, 19 sayısal kodlama sistemini işaret eden olağan dışı durumdur. Matematiksel olarak hiçbir bağlantısı olmamasına rağmen ana küme elaman sayısı (sure sayısı) olan 114 sayısının 19’un 6 katı olması ve bu sayıların açılımının aynı zamanda 60 ve 54 sayılarına sembolik olarak bağlanması ve ilişkisinin kurulabilmesi anormal veya olağanüstü bir durum olarak karşımıza çıkar. Bunu güzel bir tesadüf olarak da değerlendirebiliriz.
6 x 19 = 114 6 x ( 10 + 9 ) = 114 60 + 54 = 114
Fakat, amaç ayet sayılarını değişmesini engellemek ise, bu sembolik ilişkiler iş görecektir. Çünkü ayet sayıları değiştiğinde bu sembolik eşitlikler bozulacaktır. Bu şekilde eşitlikler kuracak şekilde küme elamanlarını seçmek bir sayısal kodlama bilgisi gerektirir.
Başka önemli görebileceğimiz konu, sayısal kodlama (şifreleme, kilitleme) sistemlerinde asal sayılar kullanılır, bu detay 20. yüzyılda teknolojinin gelişimiyle insanlığın keşfettiği bir matematik gerçeğidir. Burada 19 asal bir sayıdır. Sembolik olarak olaya yaklaştığımızda ve yukarıdaki ilk eşitliğe baktığımızda 6 19 ve 114 ü hemen fark edebiliriz. 619 sayısı da bir asal sayıdır. Hem de 114’düncü asal sayıdır. Buda iyi bir tesadüf olmuş diyebilirizzz….. mi ?!!! Tamam diyelim. Fakat unutmayalım ki bu sembolik yaklaşımlar kesinlikle iş görecek ve ayet sayılarının değişimini tesadüflerden çıkaracak ve bilgiye dayalı bir duruma getirecektir.
Simetri hesapları Aşama-2: Ayet sayılarının sayısal değerleri ve sıralaması:
İkinci aşamada analiz yapımızı biraz daha derinleştirelim. Yukarıdaki Aşama-1 de, ayet sayılarından oluşan kümenin sadece sayısal değerlerini dikkate alarak bir analiz yapmıştık. Halbuki elimizdeki kümede elemanların sayısal değerleri olduğu gibi, birde kümenin kaçıncı elemanı olduğunu barındıran başka bir bilgi daha vardır. Bu bilgi elemanın kümede kaçıncı sırada olduğunu gösterir. Bu bilgi aynı zamanda sure numarasıdır. Çünkü sure numarası ayet numaralarını indeksler, yani sırasını belirler. Biz sayısal kümeyi koruma altına almayı düşünüyorsak, kümenin eleman değerlerini ve eleman sırasını dikkate almalıyız. Bu işlemi iki veriyi birbiri ile işleme sokarak yeni bir sayı kümesi elde ederek yapabiliriz. Basit bir şekilde topladığımızı düşünelim. İranlı bir üniversite öğrencisi olan Koroş Cemnişan da öyle yapmış. Bu durumda yeni kümemiz aşağıdaki gibi oluşur;
Eleman sırası + Eleman sayısal değeri, yani Sure numaraları + Ayet sayıları;
Sure No ve Ayet Say Top = { 1 + 7 , 2 + 286 , 3 + 200, ….. , 113+5 , 114 + 6 }
Sure No ve Ayet Say Top = { 8 , 288 , 203, …… , 118 , 120 }, şeklinde yeni kümemiz oluşur. Bu yeni küme yukarıda oluşturduğumuz kümeden kodlama olarak daha etkili olduğu açıkça görülmektedir. Yeni oluşan kümeden yapacağımız kodlama elemanın sayısal değerini korumakla beraber, elemanın küme içindeki yerini de koruma altına alacaktır. Oluşan yeni kümemize yukarıda yaptığımız gibi Çift elemanların kümesi ve Tek elemanların kümesi işlemini uygulayarak yine iki alt küme elde ederiz,
Çift = { 8 , 288 , 180 , …. , 118 , 120 } Tek = { 203 , 125 , 171 , ….. , 113 }
Çift kümesi eleman toplamı = 6236 Tek kümesi eleman toplamı = 6555
Çift kümesi eleman sayısı = 57 Tek kümesi eleman sayısı = 57
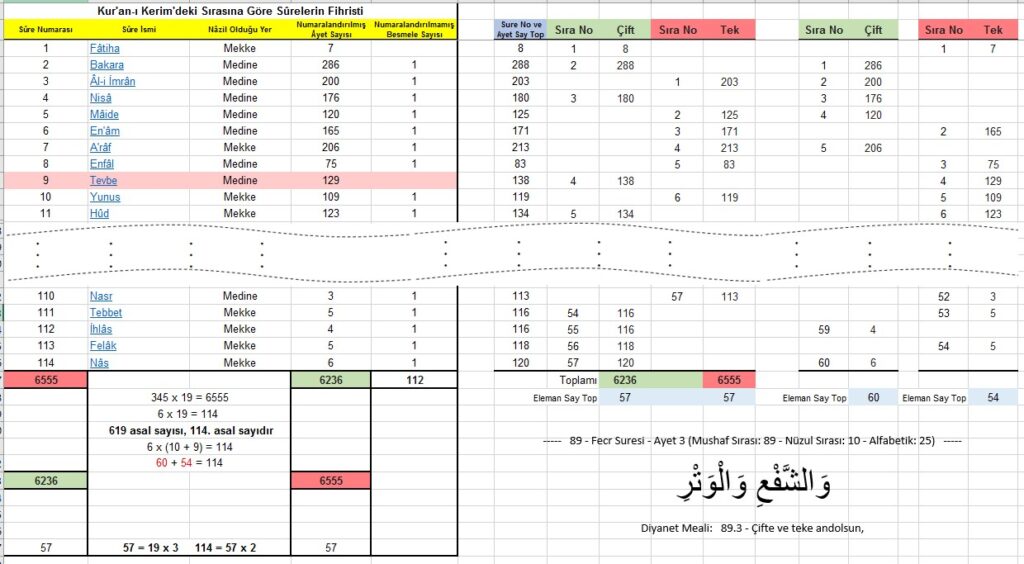
Burada karşımıza çıkan ilk normal olarak göremeyeceğimiz durum, yukarıda elde ettiğimiz Çiftlerin toplamı olan 6236 ve teklerin toplamı olan 6555 sayılarının, yine Matematiksel olarak hiçbir bağlantısı olmamasına rağmen sure sayılarının toplamı olan 6555 ile ayet sayılarının toplamı olan 6236 sayılarına eşit olmalarıdır. Bu yöntem; günümüzde bilgisayar dünyasında, gönderilen bilginin alıcı tarafından hatasız alındığını kontrol etmek için kullanılan Checksum[1] yöntemine benzetilebilir. Burada çiftlerin toplamı, ayet sayılarının toplamına ve teklerin toplamı da sure numaralarının toplamına eşit olduğunda Checksum doğrulanmış olur ve alınan bilginin bize doğru, bozulmamış olarak ulaştığını anlarız.
Ayrıca alt küme eleman sayılarının Çift, 57 ve Tek, 57 olarak eşit çıkması, kümenin eleman sayısı olarak tam ortadan ikiye ayrılması, net bir şekilde simetrik bir yapı oluşturmaktadır.
Artık ilgilendiğimiz sayı kümesinin rastgele bir sayı kümesi olmadığı, çok orijinal bir yapıya sahip olduğunu anlamaya başlarız. Kabul etmemiz gerekir ki, bu yapının tesadüf olması artık mümkün değildir. Aynı zamanda sistemimiz mükemmel bir koruma sağlayacaktır, çünkü ayet sayılarındaki ve sıralarındaki en ufacık bir değişiklik bu simetriyi etkileyecek, Checksum’ı bozacaktır. Sayı kümesinin orijinal olmadığı hemen anlaşılacaktır. Bu sayı kümesinde simetriyi bozmadan yapılacak bir değişiklik mutlaka derinlemesine bir bilgi gerektirecektir. Mushaf fihristindeki ortaya çıkan sayı kümesinin, sayısal kodlama bilgisi olmadan, tesadüfen oluşturulduğunu iddia etmek, insan aklıyla alay etmek anlamına geldiğini herkes kabul eder sanırım. 1400 sene önce oluşan bu sayı kümesi, içerdiği sayısal kodlama bilgisi sebebiyle, o devirde yaşayan insan kapasitesini aştığı çok net bellidir. Simetrik yapının yanı sıra alt kümelerin eleman sayısı olan 57 sayısının da 19 sayısal kodlama sistemine uygunluğu dikkat çekmektedir. 57 = 19 x 3. Ayrıca 114 = 57 x 2 olduğuna ve 2 sayısının ortama girdiğine dikkat edelim. Fakat şimdilik bu iki sayısının (sembolünün) nasıl ve nereyle ilişkisi olduğunu bilmiyoruz. Ek olarak küme eleman sayılarının indeksleri, yani sıra numaralarının (Sure numaraları) toplamı olan 6555 sayısının ve eleman sayısı olan 114 sayısının da 19 sayısal kodlama sistemine uyduğunu görmekteyiz. 6555 = 19 x 345 114 = 19 x 6 . Bu simetrinin ve 19 sayısal kodlama sitemine uyumun oluşması için küme elemanlarının son derece titizlikle seçilmesi ve sıralanması gerekmektedir. Yukarıda belirttiğim gibi, bu durumun normal olduğundan söz edilemez. Kesinlikle olağanüstü bir durumla karşı karşıyayız.
[1] https://wmaraci.com/nedir/checksum
Simetri hesapları Aşama-3: 60 ve 54 sayılarının alt grupları olan 30 ve 27 sayıları:
Üçüncü aşamada analiz yapımızı bir kademe daha derinleştiriyoruz. İkinci aşamada kullandığımız mantığı biraz daha sofistike kullanarak küme elemanlarının sayısal değerlerinin ve konumlarının korunmasına yönelik bir sayısal kodlama geliştirmemiz mümkündür. Küme elemanlarına (ayet sayıları) ve ayrı olarak sıra numaralarından oluşan diğer kümeye (Sure numaraları) konsantre olduğumuzda, iki kümede de Çift ve Tek sayıların olduğunu fark ederiz. O zaman yeni kümelerimizin iki boyutlu elemanları olduğunu düşünerek; yeni alt kümeleri (Sure numarası – Ayet sayısı)
Çift-Çift, Tek-Tek, Çift-Tek, Tek-Çift şeklinde oluşturabiliriz. Oluşan yapı Ayet sayılarını ve onların küme içindeki yeri olan sure numaralarını çok daha etkili bir şekilde detaylandıracak ve koruma noktasında çok daha hassas olacaktır. Değişiklikler hemen fark edilecektir. İki boyut filan dediğime bakmayın anlaşılması gayet kolay.
Yeni oluşan kümeler;
Çift-Çift={ (2, 286) , (4,176) , . . . , (112,4) , (114,6)}
Tek-Tek={ (1, 7) , (9,129) , . . . , (111,5) , (113,5)}
Çift-Tek={ (6, 165) , (8,75) , . . . , (110,3)}
Tek-Çift={ (3, 200) , (5,120) , . . . , (109,6)} şeklinde oluşur.
Tablodan daha kolay anlayabileceğinizi düşünüyorum. Bundan sonrasını direkt tablodan bakarak takip edebilirsiniz.

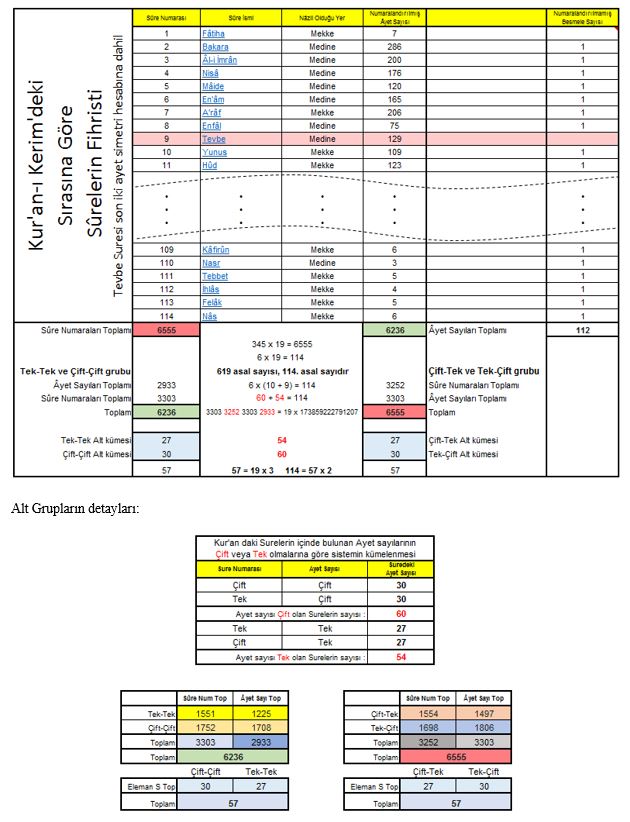
Bu sayı kümelerinin ayrı ayrı sayısal toplamlarını ve eleman sayılarını bulduğumuzda 60 olan çift sayısının 30 + 30, 54 olan tek sayısının ise 27 + 27 olarak tam yarıdan ikiye bölündüğünü görebiliriz. Toplamlarının zaten 6236 ve 6555 olduklarını bulmuştuk. Tablomuzun simetrik yapısının daha da derinleştiğini, sonuç olarak hazırladığımız sayısal kodlama sisteminin kırılmasının daha da güçleştiğini görebilirsiniz. Küme elemanlarının sayısal değerlerini ve konumlarını koruma bakımından çok etkin olduğu net bir şekilde görülmektedir. Ufak bir değişiklik toplamları değiştirecek ve simetrik denge bozulacaktır.
Burada ikinci aşamaya ek olarak alt kümelerin toplamları sayı olarak tabloya eklendi.
Yeni sayılarımız, 3303 3252 3303 2933. Bu sayıları yan yana yazarak oluşturulan sayının 19’a tam bölündüğünü söylersem şaşırmayacaksınız sanırım. Artık sistemin olağanüstü olduğunu kabul etmiş bulunuyoruz zaten. Diğer bir olağanüstülük bizi şaşırtmıyor artık. Aşağıdaki özet tabloyu vererek konumuza devam ediyorum.
Muhteşem Simetri (Son durum) Özet
Dikey Simetri (57+57): 30 + 27 ve 27 + 30

Leave a Reply